Section 1.7

Review of concepts

Definition 1

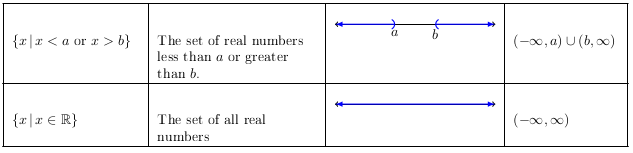
An inequality says that one expressions is:

• greater than (\(>\))

• greater than equal to (\(\ge\))

• less than (\(<\)), or

• less than equal to (\(\le\)) another expression.

Linear Inequality

First, we will look at a simple example involving inequality notations.

Example 10

Solve \(1-5x>11\).

Solution:

We solve the inequality the following way. Notice that when dividing by \(-5\) we flip the inequality.

\[\begin{align*} 1-5x & > 11\\ -5x & > 10\\ x & < -2 \end{align*}\]

Next, we consider what the graph will look like. To do this, we will test a value against the original inequality. If \(1-5x>11\) at \(x=0\) then we will graph towards zero on the number line. If the inequality is false then we graph away from zero.

Testing \(x=0\) we have:

\[\begin{align*} 1-5(0) & > 11\\ 1 & \not> 11 \end{align*}\]

This means we graph away from zero as follows:

The graph of the solution is: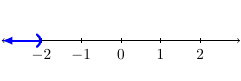

From the graph, we see the solution set is \(\{x\,|\,x<-2\}\). Also, the interval notation is \((-\infty,-2)\).

Next, we will look at a nonlinear inequality. Remember, if \(ab=0\) then \(a=0\) or \(b=0\) by the zero product property. However, we do not use this property for nonlinear inequalities.

Nonlinear Inequality

Example 11

Solve \(x^2-x-12>0\).

Solution:

First, we want to know where \(x^2-x-12\) is zero.

\[\begin{align*} x^2-x-12 & = 0\\ (x-4)(x+3) & = 0 \end{align*}\]

By the zero product property, we know \(x=4\) or \(x=-3\).

With this information we have now partitioned the real number line into three subintervals: \((-\infty,-3)\), \((-3,4)\), and \((4,\infty)\). Since the polynomial is defined everywhere and is continuous everywhere we know that if \(x^2-x-12\) is greater than zero at some point on a subinterval then the expression is greater than zero for all \(x\) values in that subinterval.

That is, we will test values in each subinterval.

• When \(x=-4\) we have \((-4)^2-(-4)-12 > 0\) which is true. This means we will shade to the left of \(x=-3\) on the number line.

• When \(x=0\) we have \((0)^2-(0)-12 > 0\) which is false. This means we will not shade the middle interval.

• When \(x=5\) we have \((5)2-(5)-12 > 0\) which is true. This means we will shade to the right of \(x=4\).

The graph of the solution should look like the following: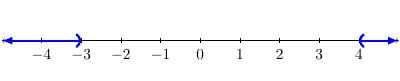

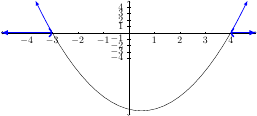
Based on the graph the solution set is \(\{x\,|\,x<-3\text{ or }4<x\}\). The interval notation would be \((-\infty,-3)\cup(4,\infty)\).

Here is a plot of \(y=x^2-x-12\) compared with the solution.

Example 12

Solve \(2x^2+5x-12\le 0\).

Solution:

First, we will solve \(2x2+5x-12 = 0\).

\[\begin{align*} 2x^2+5x-12 & = 0\\ 2x^2+8x-3x-12 & = 0\\ 2x(x+4)-3(x+4) & = 0\\ (x+4)(2x-3) & = 0 \end{align*}\]

By the zero product property, we have \(x=-4\) or \(x=\frac{3}{2}\) as solutions to the equation. Next, identify the three subintervals created by these values and put them on a number line. Since there are no other zeros for the expression and the expression is defined everywhere with no jumps we know if we test one value on a subinterval that will determine the rest of the values in the subinterval.

• When \(x=-5\) we have \(2(-5)^2+5(-5)-12\le 0\) which is flase. This means we will not shade the left-most subinterval.

• When \(x=0\) we have \(2(0)^2+5(0)-12\le0\) which is true. This means we will shade the middle subinterval.

• When \(x=2\) we have \(2(2)^2+5(2)-12\le0\) which is false. This means we will not shade the right-most subinterval.

The graph of the solution would look like: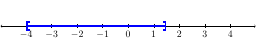

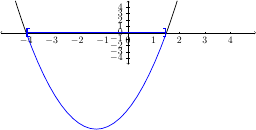
From the graph we have the solution set \(\{x\,|\,-4\le x\le \frac{3}{2}\}\) and the interval notation is \([-4,\frac{3}{2}]\).

For context, we have the following graph.

Rational Inequality

Example 13

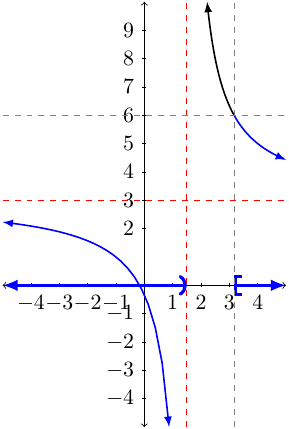
Solve \(\frac{6x+1}{2x-3} \le 6\)

Solution:

We will first solve \(\frac{6x-1}{2x-3} = 0\) like the previous examples.

\[\begin{align*} \frac{6x+1}{2x-3} & = 6\\ \frac{6x+1}{2x-3} - 6 & = 0\\ \frac{6x+1}{2x-3} - \frac{6(2x-3)}{2x-3} & = 0\\ \frac{6x+1-12x+18}{2x-3} & = 0\\ \frac{-6x+19}{2x-3} & = 0 \end{align*}\]

The solution to the equation is \(x=\frac{19}{6}\). In the past, we would say this splits the number line into 2 subintervals. However, the expression is undefined at \(x=\frac{3}{2}\). This means we must include this value on the number line. Next, we will test values.

• When \(x=0\) we have \(\frac{6(0)+1}{2(0)-3} \le 6\) which is true.

• When \(x=2\) we have \(\frac{6(2)+1}{2(2)-3} \le 6\) which is false.

• When \(x=4\) we have \(\frac{6(4)+1}{2(4)-3} \le 6\) which is true.

The graph of the solution would look like: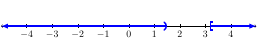

The solution set would be \(\{x\,|\,x<\frac{3}{2}\text{ or }\frac{19}{6}\le x\}\) and interval notation would be \((-\infty,\frac{3}{2})\cup[\frac{19}{6},\infty)\).

With context, we have: