Section 3.5

Definition 41 (Rational Function)

Let \(p(x)\) and \(q(x)\) be any polynomial function where \(q(x)\) is not the zero function. A rational function is

\[f(x)=\frac{p(x)}{q(x)}\]

The domain of \(f\) is the set of all \(x\) such that \(q(x)\ne0\).

When finding the domain of a rational function immediately solve \(q(x)=0\). Do not simplify \(f\) and then set the denominator equal to zero.

If \(f(x)=\frac{p(x)}{q(x)}\), then the list of possible zeros for \(f(x)\) is the zeros for \(p(x)\).

Property 6 (Graph of \(f(x)=\frac{1}{x}\).)

The graph of \(f(x)=\frac{1}{x}\) is:

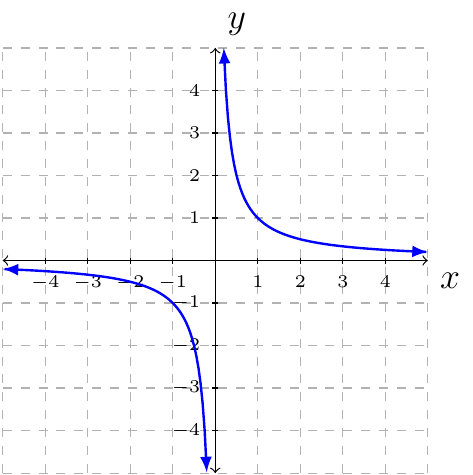
• The domain of \(f\) is the set of all \(x\) such that \(x\ne0\).

• The range of \(f\) is the set of all \(y\) such that \(y\ne0\).

• The function is continuous for all \(x\), not zero.

• The function is decreasing in its domain.

• The function has a vertical asymptote \(x=0\).

• The function has a horizontal asymptote \(y=0\).

Property 7 (Graph of \(f(x)=\frac{1}{x^2}\).)

The graph of \(f(x)=\frac{1}{x^2}\) is:

• The domain \(f\) is the set of all \(x\) such that \(x\ne0\).

• The range of \(f\) is the set of all \(y\) such that \(y\ne0\).

• The function is continuous for all \(x\), not zero.

• The function is increasing on the open interval \((-\infty,0)\).

• The function is decreasing on the open interval \((0,\infty)\).

• The function has a vertical asymptote \(x=0\).

• The function has a horizontal asymptote \(y=0\).

Definition 42 (Vertical/Horizontal Asymptote)

Let \(f(x)\) be a rational function.

• If the size of \(f(x)\) approaches infinity as \(x\) approaches a fixed number (say \(a\)). Then we say \(f\) has a vertical asymptote at \(x=a\).

• If \(f(x)\) approaches a number \(L\) as \(x\) approaches infinity. Then \(f\) has a horizontal asymptote at \(y=L\).

• If \(f(x)\) approaches a number \(M\) as \(x\) approaches negative infinity. The \(f\) has a horizontal asymptote at \(y=M\).

When finding the domain of a rational function do not simplify. When finding vertical or horizontal asymptote(s) first simplify.

Important facts when dealing with a horizontal asymptote. The function \(\frac{1}{x}\) approaches zero when \(x\) approaches \(\infty\).

Example 62

Let \(f(x)=\frac{x+1}{(2x-1)(x+3)}\).

Find the domain of the function.

Solution:

Immediately setting the denominator equal to zero we say \(x\) cannot be \(\frac{1}{2}\) or \(-3\). Therefore, the domain of \(f\) is the set of all \(x\) such that \(x\ne\frac{1}{2}\) or \(x\ne-3\) (interval notation would be \((-\infty,-3)\cup(-3,\frac{1}{2})\cup(\frac{1}{2},\infty)\).

Find the vertical asymptote.

Solution:

Since \(f\) is already simplified and the denominator is zero when \(x\) is \(\frac{1}{2}\) or \(-3\) we say \(f\) has vertical asymptote \(y=\frac{1}{2}\) and \(y=-3\).

Find the horizontal asymptote.

Solution:

First, we will write the function in the following way:

\[\begin{align*} f(x) & = \frac{x+1}{(2x-1)(x+3)}\\ & = \frac{x+1}{2x^2+5x-3} \end{align*}\]

Next, we divide the top and bottom by \(x^2\).

\[\begin{align*} \frac{x+1}{2x^2+5x-3} & = \frac{\frac{1}{x}+\frac{1}{x^2}}{2+\frac{5}{x}-\frac{3}{x^2}}\\ & \to \frac{0+0}{2+0-0} = 0 \end{align*}\]

Therefore, the function has a horizontal asymptote \(x=0\).

Example 63

Let \(f(x)=\frac{2x+1}{x-3}\). Find horizontal and vertical asymptotes.

Horizontal Asymptote:

Solution:

First, divide the top and bottom by \(x\).

\begin{align*) \frac{2x+1}{x-3} & = \frac{2+\frac{1}{x}}{1-\frac{3}{x}}\ & \to \frac{2+0}{1-0} = 2 \end{align*}

As \(x\to0\) we see that \(f(x)\to0\). Therefore, \(f\) has horizontal asymptote \(y=2\).

Vertical Asymptote:

Solution:

Since \(f\) is fully simplified and \(x-3=0\) when \(x=3\) we say the line \(x=3\) is a vertical asymptote.

Example 64

Let \(f(x)=\frac{x^2+x-6}{x^2-x-12}\). Find horizontal and vertical asymptotes.

Before moving forwards, we should first simplify \(f\).

Solution:

\[\begin{align*} \frac{x^2+x-6}{x^2-x-12} & = \frac{(x+3)(x-2)}{(x-4)(x+3)}\\ & = \frac{x-2}{x-4} \end{align*}\]

Horizontal asymptote:

Solution:

First, we will divide the top and bottom by \(x\).

\[\begin{align*} \frac{x-2}{x-4} & = \frac{1-\frac{2}{x}}{1-\frac{4}{x}}\\ & \to \frac{1-0}{1-0}=1 \end{align*}\]

That is, \(f\to 1\) as \(x\to \infty\). Therefore, \(f\) has a horizontal asymptote \(y=1\).

Vertical asymptote:

Solution:

Since \(f\) simplified is \(\frac{x-2}{x-4}\) and \(x-4=0\) whenever \(x=4\); we say, \(x=4\) is a vertical asymptote.

In the last example it is important to note that \(f(x)\ne\frac{x-2}{x-4}\) and \(f(-3)\) is undefined (point-wise). If you graph \(y=\frac{x^2+x-6}{x^2-x-12}\) and \(y=\frac{x-2}{x-4}\) you will think they are the same; however, they are not. The graph \(y=\frac{x^2+x-6}{x^2-x-12}\) will have a hole when \(x=-3\). The graph \(y=\frac{x-2}{x-4}\) will not have a hole when \(x=-3\).

Example 65

Find the oblique asymptote for the function \(f(x)=\frac{x^2+1}{x-2}\).

Solution:

After polynomial long division we have:

\[\frac{x^2+1}{x-2} = x+2+\frac{5}{x-2}\]

Therefore, the oblique asymptote is \(y=x+2\). That is, the graph \(y=\frac{x^2+1}{x-2}\) will always approach the line \(y=x+2\) but never touch it.