Section 2.5

Consider a fixed point on a line and call it \((x_1,y_1)\). Next, consider any other point on the line and call it \((x,y)\). Then the slope of the line would be:

\[m=\frac{y-y_1}{x-x_1}\]

The equivalent equation would be: \(y-y_1=m(x-x_1)\); provided \((x,y)\) is not the fixed point. This leads to the point-slope form equation of a line.

Point-Slope Form

Definition 14 (Point-Slope Form)

The point-slope form of the equation of a line with a slope of \(m\) and a point \((x_1,y_1)\) is

\[y-y_1=m(x-x_1)\]

Examples

Example 28

Write the equation of a line passing through the point \((-4,1)\) and a slope of \(3\). Finish the equation in slope-intercept form (\(y=mx+b\)).

Solution:

We are given \((x_1,y_1)=(-4,1)\) and \(m=3\). Plugging these values into the point-slope form equation we have:

\[y-1=3(x+4)\]

Now, solve for \(y\) to get into slope-intercept form

\[\begin{align*} y-1 & = 3(x+4)\\ y-1 & = 3x+12\\ y & = 3x+12+1\\ & = 3x+13 \end{align*}\]

Therefore, the equation of the line passing through \((-4,1)\) and having a slope of \(3\) is: \(y=3x+13\).

Example 29

Write the equation of the line passing through the points \((-4,3)\) and \((5,-1)\). Finish the equation in slope-intercept form (\(y=mx+b\)).

Solution:

We are given \((x_1,y_1)=(-4,3)\) and \((x_2,y_2)=(5,-1)\). To find the equation of the line we must first find the slope of the line. Using \(m=\frac{y_2-y_1}{x_2-x_1}\) we have

\[\begin{align*} m & = \frac{-1-3}{5-(-4)}\\ & = \frac{-4}{9} \end{align*}\]

Next, we pick one of the two points, \((-4,3)\), and use \(m=-\frac{4}{9}\) to find the equation of the line:

\[\begin{align*} y-3 & =-\frac{4}{9}(x+4)\\ y-3 & = -\frac{4}{9}x-\frac{16}{9}\\ y & = -\frac{4}{9}x +\frac{27-16}{9}\\ & = -\frac{4}{9}x + \frac{11}{9} \end{align*}\]

Therefore, the equation of the line is \(y=-\frac{4}{9}x+\frac{11}{9}\).

Example 30

Given the following graph. Find the equation of the line.

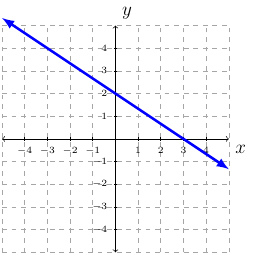
Solution:

One way to find the equation of the line is to have two points, find the slope, plug the point and slope into the point-slope, and then solve for \(y\). Given the graph, we have many points to choose from. However, two points are clearly on the line: \((0,2)\) and \((3,0)\). We will use these points to find the equation of the line. First, we will find the slope:

\[\begin{align*} m & = \frac{0-2}{3-0}\\ & = \frac{-2}{3} \end{align*}\]

Using the point \((0,2)\) and slope \(m=-\frac{2}{3}\) we have:

\[\begin{align*} y-2&=-\frac{2}{3}(x-0)\\ y & = -\frac{2}{3}x+2 \end{align*}\]

Therefore, the equation of the graphed line is: \(y=-\frac{2}{3}x+2\).

Horizontal and Vertical Lines

Definition 15 (Vertical and Horizontal Lines)

• An equation of the vertical line through the point \((a,b)\) is \(x=a\).

• An equation of the horizontal line through the point \((a,b)\) is \(y=b\).

Parallel and Perpendicular Lines

Definition 16 (Parallel and Perpendicular Lines)

• Two distinct nonvertical lines are parallel if and only if they have the same slope.

• Two lines, neither of which is vertical, are perpendicular if and only if their slopes have a product of \(-1\).

It is common to say if the slope of line one is \(m_1\), then the slope of the perpendicular line is the opposite reciprocal. That is, \(m_2=\frac{1}{m_2}\).

Examples

Example 31

Let line one be \(y=3x+10\).

• if line two is parallel to line one, then the slope of line two would be \(m=3\).

• if line two is perpendicular to line one, then the slope of line two would be \(m=-\frac{1}{3}\).

Example 32

Write an equation in slope-intercept form of the line that passes through the point \((2,-4)\) and satisfies the given conditions.

Parallel to the line \(3x-2y=5\).

Solution:

To construct a line equation we need a point and a slope. We know the point is \((2,-4)\). Next, we need to find the slope of the new line.

The slope of the old line is unknown as the equation is given. We must first find the slope-intercept form of the equation given to find the slope of the old line.

\[\begin{align*} 3x-2y & = 5\\ 2y & = 3x-5\\ y & = \frac{3}{2}x-\frac{5}{2} \end{align*}\]

From this, we see the slope of the old line is \(m=\frac{3}{2}\). This means the slope of the new line, parallel to the old line, must be \(m=\frac{3}{2}\).

Since, we have \((x_1,y_1)=(2,-4)\) and \(m=\frac{3}{2}\) we can now find the equation of the line.

\[\begin{align*} y+4 & = \frac{3}{2}(x-2)\\ y & = \frac{3}{2}x-3-4\\ & = \frac{3}{2}x-7 \end{align*}\]

Therefore, the equation of the line parallel to \(3x-2y=5\) and passes through the point \((2,-4)\) is \(y=\frac{3}{2}x-7\).

Perpendicular to the line \(3x-2y=5\).

Solution:

Given: \((x_1,y_1)=(2,-4)\)

Since \(3x-2y=5\) can be written as \(y=\frac{3}{2}x-7\) we know the slope of the old line is \(m=\frac{3}{2}\).

The slope of the new line is \(m=-\frac{2}{3}\) since the slope of the old line was \(m=\frac{3}{2}\).

All together we have:

\[\begin{align*} y+4 & =-\frac{2}{3}(x-2)\\ y & = -\frac{2}{3}x + \frac{4}{3} - 4\\ & = -\frac{2}{3}x + \frac{4-12}{3}\\ & = -\frac{2}{3}x - \frac{8}{3} \end{align*}\]

Therefore, the equation of the line perpendicular to \(3x-2y=5\) and passes through the point \((2,-4)\) is \(y=-\frac{2}{3}x-\frac{8}{3}\).