Section 2.6

Continuity

Definition 17

A function is continuous over an interval of its domain if its hand-drawn graph over that interval can be sketched without lifting the pencil from the paper.

Basic Graphs and Information

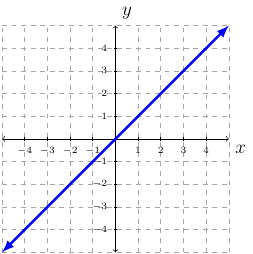
Definition 18 (Identity Function)

Identity Function: \(f(x)=x\).

• Domain is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Range is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Continuous everywhere or \((-\infty,\infty)\).

• Increasing everywhere or \((-\infty,\infty)\).

• 

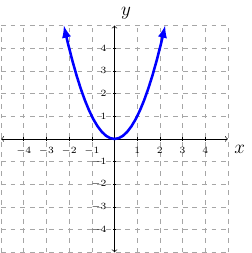
Definition 19 (Squaring Function)

Squaring Function: \(f(x)=x^2\).

• Domain is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Range is \([0,\infty)\).

• Contiuous everywhere or \((-\infty,\infty)\).

• Decreasing on \((-\infty,0)\).

• Increasing on \((0,\infty)\).

• 

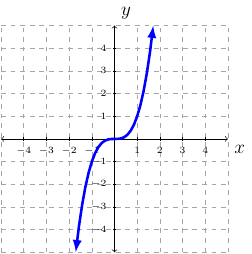
Definition 20 (Cubing Function)

Cubing Function: \(f(x)=x^3\)

• Domain is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Range is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Continuous everywhere or \((-\infty,\infty)\).

• Increasing everywhere or \((-\infty,\infty)\).

• 

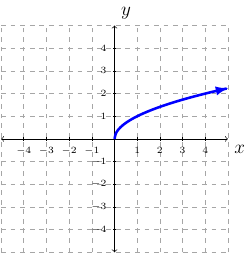
Definition 21 (Square Root Function)

Square Root Function: \(f(x)=\sqrt{x}\).

• Domain is \([0,\infty)\).

• Range is \([0,\infty)\).

• Continuous on \([0,\infty)\).

• Increasing on \((0,\infty)\).

• 

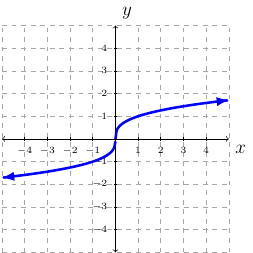
Definition 22 (Cube Root Function)

Cube Root Function: \(f(x)=\sqrt[3]{x}\)

• Domain is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Range is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Continuous everywhere or \((-\infty,\infty)\).

• Increasing everywhere or \((-\infty,\infty)\).

• 

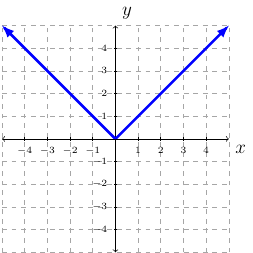
Definition 23 (Absolute Value Function)

Absolute Value Function: \(f(x)=|x|\).

• Domain is \(\mathbb{R}\) or \((-\infty,\infty)\).

• Range is \([0,\infty)\).

• Continuous everywhere or \((-\infty,\infty)\).

• Decreasing on \((-\infty,0)\).

• Increasing on \((0,\infty)\).

•