Section 1.8

Review

$$\begin{array}{r}|x|=\{\begin{array}{cc}x& x\le 0\\ -x& x>0\end{array}\end{array}$$

Remember that the absolute value doesn’t just change a negative number to a positive one. The absolute value of a number is the distance the number is away from zero. Another way to write the absolute value of a number is $x=\sqrt{x^2}$.

• Given, $|x|=k$, the graph would look like: 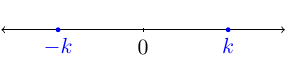and the set would $\{-k,k\}$.

• Given, $|x|<k$, the graph would look like: 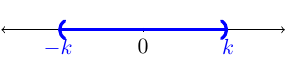and the interval notation would be $(-k,k)$.

• Given, $|x|>k$, the graph would look like: and the interval notation would be $(-\mathrm{\infty },-k)\cup (k,\mathrm{\infty })$.

Absolute Value Equations

Example 14

Solve $|9-4x|=7$

Solution:

Remember $|X|=k$ if and only if $X=-k$ or $X=k$. This means we will create two equations to solve:

$$\begin{array}{rlrl}9-4x& =7& 9-4x& =-7\\ -4x& =-2& -4x& =-16\\ x& =\frac{1}{2}& x& =4\end{array}$$

Therefore, the solution set for the equation is $\{\frac{1}{2},4\}$.

Remember, the absolute value expression must be isolated before splitting into two equations.

Example 15

Solve $|2x+3|+1=5$

Solution:

First, we need to isolate the absolute value expression:

$$\begin{array}{rl}|2x+3|+1& =5\\ |2x+3|=4\end{array}$$

Next, we split the equation into two equations. That is, we what to know when $2x+3$ is equal to $4$ and $-4$.

$$\begin{array}{rlrl}2x+3& =4& 2x+4& =-4\\ 2x& =1& 2x& =-7\\ x& =\frac{1}{2}& x& =-\frac{7}{2}\end{array}$$

Therefore, the solution set is $\{\frac{1}{2},-\frac{7}{2}\}$.

Absolute Value Inequality

Remember the absolute value of some number, $X$, is the distance $X$ is away from zero. When it comes to inequalities we want to know the collection of numbers that satisfies the conditions.

$|X|<k$

Remember when we have $|X|<k$ we want to find all $X$ values such that the size of $X$ is smaller than $k$.

Example 16

Solve $|4x+3|<10$

Solution:

For this inequality, we want to know when $4x+3>-10$ and $4x+3<10$. It is important to understand why geometrically. Solving the two inequalities we have

$$\begin{array}{rlrl}4x+3& >-10& 4x+3& <10\\ 4x& >-13& 4x& <7\\ x& >-\frac{13}{4}& x& <\frac{7}{4}\end{array}$$

We then graph this solution: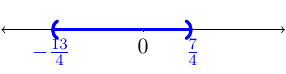

The solution in interval notation would be $(-\frac{13}{4},\frac{7}{4})$.

$|X|>k$

Remember when we have $|X|>k$ we want to find all $X$ values such that the size of $X$ is bigger than $k$.

Example 17

Solve $|5x+10|>5$

Solution:

Here we want to find all the $x$ such that the size of $5x+10$ is larger than $5$ units away from zero. That is, we want to solve these two inequalities: $5x+10>5$ and $5x+10<-5$.

$$\begin{array}{rlrl}5x+10& >5& 5x+10& <-5\\ 5x& >-5& 5x& <-15\\ x& >-1& x& <-3\end{array}$$

The graph of the solution would be: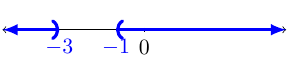

The solution in interval notation would be $(-\mathrm{\infty },-1)\cup (-3,\mathrm{\infty })$.