Section 4.3

Definition and Properties

The exponential function is \(f(x)=a^x\).

Let \(f(x)=2^x\). Consider \(f(2)=2^2=4\) and \(f(3)=2^3=8\). Since \(f\) is continuous on \([2,3]\), \(f(2)=4\), and \(f(3)=8\), we know, by the intermediate value theorem there exists a \(c\) in \([2,3]\) such that \(f(c)=7\). In fact, there is a number such that \(2^x\) is 5,6, or 7.

Remember, \(\sqrt{4}=2\) because \(2^2=4\). We want to find/name a function such that \(f(8)=3\) because \(2^3=8\).

Definition 49

For all real numbers \(y\) and all positive numbers \(a\) and \(x\), where \(a\ne 1\). Then \(y=\log_a (x)\) if and only if \(x=a^y\).

Like, \(\sqrt{4}=2\) because \(2^2=4\) we have: \(3=\log_2(8)\) because \(2^4=8\).

Definition 50

If \(a>0\), \(a\ne 1\) and \(x>0\), then the logarithm function with base \(a\) is

\[f(x)=\log_a(x)\]

• The domain is \((0,\infty)\) (which is the range of \(a^x\) function).

• The range is \((-\infty,\infty)\) (which is the domain of \(a^x\) function).

• The function \(f\) is continuous on \((0,\infty)\).

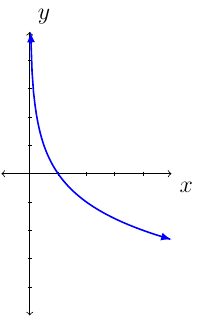
• If \(0<a<1\), then \(f\) is decreasing on its domain.

• if \(a>1\), then \(f\) is increasing on its domain.

• The graph of \(f\) has vertical asymptote \(x=0\).

• The graph passes through \((\frac{1}{a},-1)\), \((1,0)\), and \((a,1)\).

The graph of the logarithmic function changes based on the value of \(a\).

The graph of \(f(x)=\log_a(x)\) when \(a>1\) we have:

The graph of \(f(x)=\log_a(x)\) where \(0<a<1\) we have:

If \(f(x)=a^x\) then \(f^{-1}(x)=\log_a(x)\). Therefore, by definition, we have:

\[a^{\log_a(x)}=x\]

and

\[\log_a(a^x)=x\]

• Since \(a^1=a\) we have \(\log_a(x)=1\).

• Since \(a^0=1\) where \(a\ne 0\) we have \(\log_a(1)=0\).

Property 13 (Laws of Logarithms)

Let \(A\), \(B\), and \(a\) be positive real numbers where \(a\ne 1\).

• \(\log_a(AB)=\log_a(A)+\log_a(B)\)

• \(\log_a(\frac{A}{B}) = \log_a(A)-\log_a(B)\)

• \(\log_a(A^n) = n\log_a(A)\)

Examples

Example 71

Use the properties of the logarithm to expand the following expression. Assume all variables are positive.

\[\log_a\left(\sqrt[3]{\frac{x^2y}{z^3}}\right)\]

Solution:

\[\begin{align*} \log_{a}\left(\frac{x^{2}y}{z^{3}}\right) & =\log_{a}(x^{2}y)-\log_{a}(z^{3})\\ & =\log_{a}(x^{2})+\log_{a}(y)-3\log_{a}(z)\\ & =2\log_{a}(x)+\log_{a}(y)-3\log_{a}(z) \end{align*}\]

Example 72

Use logarithm properties to write the expression as a single logarithm with coefficient one. Assume all variables are positive.

\[\frac{1}{2}\log_a(x)+\log_a(y)-4\log_a(z)\]

Solution:

\[\begin{align*} \frac{1}{2}\log_a(x)+\log_a(y)-4\log_a(z) & = \log_a(x^{\frac{1}{2}})+\log_a(y)-\log_a(z^4)\\ & = \log_a(\sqrt{x}\cdot y)-\log_a(z^4)\\ & = \log_a(\frac{y\sqrt{x}}{z^4}) \end{align*}\]

Example 73

Let \(\log_{10}(7)\approx 0.8451\). Evaluate the following:

Approximate \(\log_{10}(49)\).

Solution:

\[\begin{align*} \log_{10}(49) & = \log_{10}(7^2)\\ & = 2\log_{10}(7)\\ & \approx 2(0.8451)\\ & = 1.6902 \end{align*}\]

Approximate \(\log_{10}(70)\).

Solution:

\[\begin{align*} \log_{10}(70) & = \log_{10}(7\cdot 10)\\ & = \log_{10}(7) + \log_{10}(10)\\ & \approx 0.8451 + 1\\ & = 1.8451 \end{align*}\]

More Examples

Example 74

Use properties of logarithms to rewrite the expression. Assume all variables are positive.

\[\log_b\left(\frac{rs^2t}{u^3v^5}\right)\]

Solution:

\[\begin{align*} \log_b\left(\frac{rs^2t}{u^3v^5}\right) & = \log_b(rs^2t)-\log_b(u^3v^5)\\ & = \left(\log_b(r)+\log_b(s^2)+\log_b(t)\right)-\left(\log_b(u^3)+\log_b(v^5)\right)\\ & = \log_b(r)+2\log_b(s)+\log_b(t)-3\log_b(u)-5\log_b(v) \end{align*}\]

Example 75

Write the expression as a single logarithm with a coefficient of 1. Assume all variables represent positive real numbers.

\[\frac{1}{3}\log_a(x)+\frac{2}{3}\log_a(y)-\log_a(xy)\]

Solution:

\[\begin{align*} \frac{1}{3}\log_{a}(x)+\frac{2}{3}\log_{a}(y)-\log_{a}(xy) & =\log_{a}(x^{\frac{1}{3}})+\log_{a}(y^{\frac{2}{3}})-\log_{a}(xy)\\ & =\log_{a}(\sqrt[3]{x}\cdot\sqrt[3]{y^{2}})-\log_{a}(xy)\\ & =\log_{a}(\sqrt[3]{xy^{2}})-\log_{a}(xy)\\ & =\log_{a}\left(\frac{\sqrt[3]{xy^{2}}}{xy}\right) \end{align*}\]

Example 76

Solve the equation.

\[x=\log_5(\frac{1}{625})\]

Solution:

\[\begin{align*} x & = \log_5(\frac{1}{625})\\ & = \log_5(1)-\log_5(625)\\ & = 0-\log_5(5^4)\\ & = -4\log_5(5)\\ & = -4(1) \text{ or } -4 \end{align*}\]

Remember \(a^{\log_a(x)}=x\) and \(\log_a(a^x)=x\).

Example 77

Solve \(\log_{\frac{1}{2}}(x+3)=-4\).

Solution:

Remember \(\left(\frac{1}{2}\right)^{\log_{\frac{1}{2}}(x)}=x\). This also means:

\[\left(\frac{1}{2}\right)^{\log_{\frac{1}{2}}(x+3)}=x+3\]

The equation \(\log_{\frac{1}{2}}(x+3)=-4\) will be composed both sides by the exponential function base \(\frac{1}{2}\).

\[\begin{align*} \log_{\frac{1}{2}}(x+3) & = -4\\ \left(\frac{1}{2}\right)^{\log_{\frac{1}{2}}(x+3)} & = \left(\frac{1}{2}\right)^{-4}\\ x+3 & = 16\\ x & = 13 \end{align*}\]

Like square root equations, we must check the solution:

\[\begin{align*} \log_{\frac{1}{2}}(13+3) & = \log_{\frac{1}{2}}(16)\\ & = \log_{\frac{1}{2}}(2^4)\\ & = \log_{\frac{1}{2}}(\frac{1}{2^{-4}})\\ & = \log_{\frac{1}{2}}(\left(\frac{1}{2}\right)^{-4})\\ & = -4\log_{\frac{1}{2}}(\frac{1}{2})\\ & = -4 \end{align*}\]

This verifies the equation.

Example 78

Let \(f(x)=5^x+1\). Find \(f^{-1}(x)\).

Solution:

First, \(y=5^x+1\) and swap the \(x\) and \(y\) variables. Then solve for \(y\). Remember \(\log_5(5^x)=x\) and \(\log_5(5)=1\).

\[\begin{align*} x & = 5^y + 1\\ x-1 & = 5^y\\ \log_5(x-1) & = \log_5(5^y)\\ \log_5(x-1) & = y\log_5(5)\\ \log_5(x-1) & = y \end{align*}\]

This means, \(f^{-1}(x)=\log_5(x-1)\).

Example 79

Let \(f(x)=\log_{10}(2x)\). Find \(f^{-1}(x)\).

Solution:

First, \(y=\log_{10}(2x)\) and swap the \(x\) and \(y\) variables. Then solve for \(y\). Remember \(10^{\log_{10}(x)}=x\).

\[\begin{align*} x & = \log_{10}(2y)\\ 10^x & = 10^{\log_{10}(2y)}\\ 10^x & = 2y\\ \frac{1}{2}\cdot 10^x & = y \end{align*}\]

This means, \(f^{-1}(x)=\frac{1}{2}\cdot 10^x\).

Example 80

Solve \(\left(\frac{1}{3}\right)^{x+1}=9^x\).

Solution:

First, we will want to rewrite the equation as an exponential expression base \(3\).

\[\begin{align*} \left(\frac{1}{3}\right)^{x+1} & = 9^x\\ \left(3^{-1}\right)^{x+1} & = \left(3^2\right)^x\\ 3^{-x-1} & = 3^{2x} \end{align*}\]

Next, use the fact \(\log_3(3^x)=x\).

\[\begin{align*} 3^{-x-1} & = 3^{2x}\\ \log_3\left(3^{-x-1}\right) & = \log_3\left(3^{2x}\right)\\ -x-1 & = 2x\\ -1 & = 3x\\ x & = -\frac{1}{3} \end{align*}\]