Section 1.1

Definition 1 (Angles)

Two distinct points \(A\) and \(B\) where a line passes through them is called \(\overleftrightarrow{AB}\).

The portion of the line between \(A\) and \(B\), including \(A\) and \(B\), is called a line segement, denoted \(\overline{AB}\).

The portion of the line \(\overleftrightarrow{AB}\) that starts at \(A\) and passes through \(B\) is called the ray \(\overrightarrow{AB}\). The point \(A\) is called the end point.

An angle consists of two rays in a plane with a common end point.

An angle consists of two rays in a plane with a common endpoint, or two line segments with a common endpoint. Each of these two rays (or segments) are called sides of the angle. The common endpoint is called the vertex. Angle is measured by rotating a ray starting at one side (the initial side) and ending at the other side (the terminal side). The positive direction of this rotation is counter-clockwise. It is also possible to complete more than one revolution.

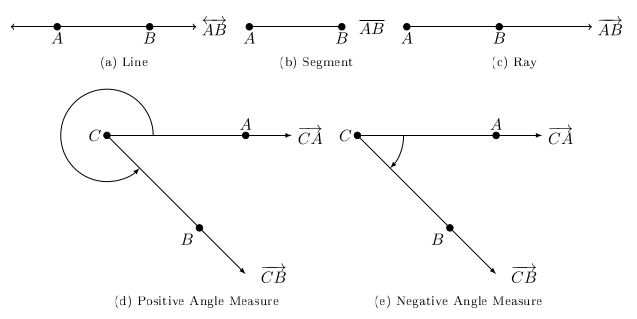
'images of the different definition on lines and angles'

The notation \(m(\angle A)\) is ``the measure of angle \(A\)’’ where \(A\) is the endpoint and vertex to the two existing rays.

There are 360 equal partitions to complete a single rotation, we call these partitions degrees. Each degree has 60 equal partitions called minutes*. Each minute has 60 equal partitions called seconds.

An angle measuring between \(0^{\circ}\) and \(90^{\circ}\) is an acute angle. An angle measuring exactly \(90^{\circ}\) is a right angle. An angle measuring more than \(90^{\circ}\) but less than \(180^{\circ}\) is an obtuse angle. An angle measuring exactly \(180^{\circ}\) is a straight angle.

When the sum of two angles equal \(90^{\circ}\) we say they are complementary and the two angles are complements of each other.

When the sum of two angles equal \(180^{\circ}\) we they are supplementary and the two angles are supplements of each other.

\[\begin{align*} 1^{\circ} & =\dfrac{1}{360}\text{ revolutions}\\ 1' & =1\text{ minute}=\left(\dfrac{1}{60}\right)^{\circ}\\ 1'' & =1\text{ second}=\left(\dfrac{1}{60}\right)'=\left(\dfrac{1}{3600}\right)^{\circ} \end{align*}\]

An angle in standard position if its vertex is at the origin and its initial side lies on the positive \(x\)-axis.

Angle measures that differ by a multiple of \(360^{\circ}\) are coterminal angles.