Section 2.1

Given the following triangle, we have the right-triangle-based definition of trigonometric functions.

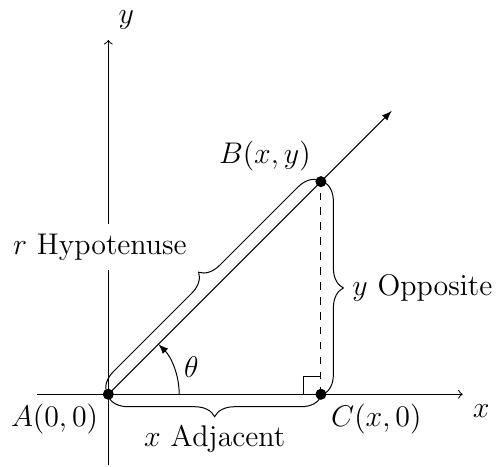
Definition 5

Let \(A\) represent any acute angle in standard position. Then

\[\begin{align*} \sin\theta & =\dfrac{y}{r}=\dfrac{\text{side opposite A}}{\text{hypotenuse}} & \cos\theta & =\dfrac{x}{r}=\dfrac{\text{side adjacent to A}}{\text{hypotenuse}} & \tan\theta & =\dfrac{y}{x}=\dfrac{\text{side opposite A}}{\text{side adjacent A}}\\ \csc\theta & =\dfrac{r}{y}=\dfrac{\text{hypotenuse}}{\text{side opposite A}} & \sec\theta & =\dfrac{r}{x}=\dfrac{\text{hypotenuse}}{\text{side adjacent to A}} & \cot\theta & =\dfrac{x}{y}=\dfrac{\text{side adjacent to A}}{\text{side opposite A}} \end{align*}\]

Theorem 4 (Cofunction Identities)

Let \(\theta\) represent any acute angle. Then the following hold true:

\[\begin{align*}\sin\theta & =\cos(90^{\circ}-\theta) & \cos\theta & =\sin(90^{\circ}-\theta) & \tan\theta & =\cot(90^{\circ}-\theta)\\ \csc\theta & =\sec(90^{\circ}-\theta) & \sec\theta & =\csc(90^{\circ}-\theta) & \cot\theta & =\tan(90^{\circ}-\theta) \end{align*}\]

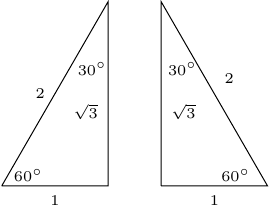
The following is a \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) right triangle which will be used to define the following:

\[\begin{align*} \cos(30^{\circ}) & = \frac{\sqrt{3}}{2} & \sin(30^{\circ}) & = \frac{1}{2}\\ \cos(60^{\circ}) & = \frac{1}{2} & \sin(60^{\circ}) & = \frac{\sqrt{3}}{2} \end{align*}\]

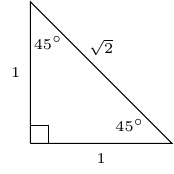
The following is a \(45^{\circ}\) - \(45^{\circ}\) - \(90^{\circ}\) right triangle which will be used to define the following:

\[\begin{align*} \cos(45^{\circ}) & = \frac{\sqrt{2}}{2} & \sin(45^{\circ}) & = \frac{\sqrt{2}}{2} \end{align*}\]

Therefore, from last chapter and this section we have the following:

\(\theta\)	\(\cos(\theta)\)	\(\sin(\theta)\)
\(0^{\circ}\)	\(1\)	\(0\)
\(30^{\circ}\)	\(\frac{\sqrt{3}}{2}\)	\(\frac{1}{2}\)
\(45^{\circ}\)	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{2}}{2}\)
\(60^{\circ}\)	\(\frac{1}{2}\)	\(\frac{\sqrt{3}}{2}\)
\(90^{\circ}\)	\(0\)	\(1\)

Using the reciprocal and quotient identities we know know the values of all six trig functions at 0, 30,45, 60, and 90 degrees.