Section 3.1

Definition 7 (Radians)

An angle with its vertex at the center of a circle that intercepts an arc on the circle equal in length to the radius of the circle has a measure of 1 radian.

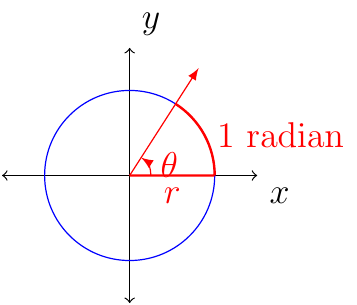
Given that \(360^{\circ}=2\pi\text{ radians}\) for simplicity we notice that \(180^{\circ}=\pi\text{ radians}\). This means that

\[ 1^{\circ}=\dfrac{\pi}{180}\text{ radians} \]

and

\[ 1\text{ radians }=\left(\dfrac{180}{\pi}\right)^{\circ} \]

Example 17

Convert from one unit to another.

\(30^{\circ}\)

Solution:

\[30\cdot\frac{\pi}{180}=\frac{\pi}{6}\]

\(\frac{2\pi}{3}\) radians

Solution:

\[\frac{2\pi}{3}\cdot\frac{180}{\pi}=120\]

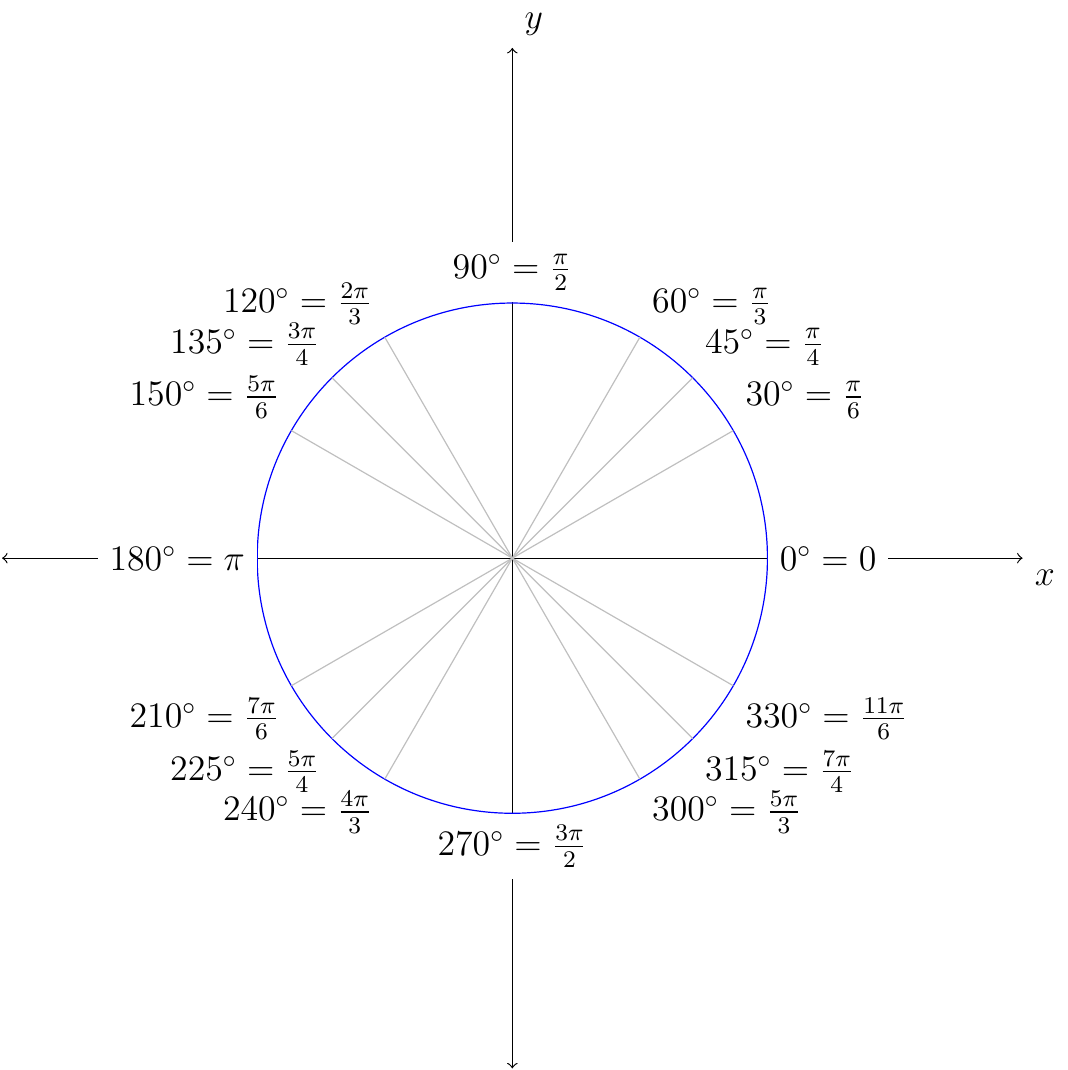
Example 18

Evaluate the following:

\(\cos(\frac{\pi}{6})\)

Solution:

\[\cos(\frac{\pi}{6})=\cos(30^{\circ})=\frac{\sqrt{3}}{2}\]

\(\sin(\frac{\pi}{4})\)

Solution:

\[\sin(\frac{\pi}{4})=\sin(45^{\circ})=\frac{\sqrt{2}}{2}\]

\(\cos(\frac{7\pi}{6})\)

Solution:

Notice that \(\frac{7\pi}{6}\) is in quadrant III, the reference angle is \(\frac{\pi}{6}\), and \(\cos(\theta)<0\) when \(\theta\) is in quadrant III:

\[\begin{align*} \cos(\frac{7\pi}{6}) & =-\cos(\frac{\pi}{6})\\ & =-\cos(30^{\circ})\\ & =-\frac{\sqrt{3}}{2} \end{align*}\]

\(\tan(\frac{5\pi}{3})\)

Solution:

Notice that \(\frac{5\pi}{3}\) is in quadrant IV, the reference angle is \(\frac{\pi}{3}\), and \(\tan(\theta)<0\) when \(\theta\) is in quadrant IV:

\[\begin{align*} \tan(\frac{5\pi}{3}) & =-\tan(\frac{\pi}{3})\\ & =-\tan(60^{\circ})\\ & =-\dfrac{\sin(60^{\circ})}{\cos(60^{\circ})}\\ & =-\dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\\ & =-\sqrt{3} \end{align*}\]