Section 2.5

Example 13

Building B is shorter than Building A. Standing on top of Building B (and closest corner to Building B) there is an angle of elevation of \(60^{\circ}\) from the top of Building B to the top of Building A. There is an angle of depression from the top of Building B to the bottom of Building A of \(30^{\circ}\). If Building A is \(100\) meters tall then how tall is Building B?

Solution:

First, we will draw a picture.

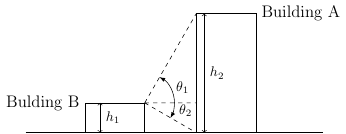
We want to solve for \(h_1\).

We know that the difference between the heights of the two buildings is \(\Delta h=h_{2}-h_{1}\) and it’s positive because \(h_{2}>h_{1}\). This means that \(h_{1}=h_{2}-\Delta h\) where \(h_{2}=100\) which is given. Let \(\Delta x\) be the distance between the two building on the horizontal axis. Then we know

\[ \tan(\theta_{1})=\dfrac{\Delta h}{\Delta x}\text{ and }\tan(\theta_{2})=\dfrac{h_{1}}{\Delta x} \]

\[\begin{split} \begin{cases} \Delta x & =\dfrac{\Delta h}{\tan(\theta_{1})}\\ \Delta x & =\dfrac{h_{1}}{\tan(\theta_{2})} \end{cases} \end{split}\]

Since the distance between the two building is the same we have

\[\begin{align*} \dfrac{\Delta h}{\tan(\theta_{1})}=\dfrac{h_{1}}{\tan(\theta_{2})} & \to\dfrac{h_{2}-h_{1}}{\tan(\theta_{1})}=\dfrac{h_{1}}{\tan(\theta_{2})}\\ & \to\dfrac{h_{2}}{\tan(\theta_{1})}-\dfrac{h_{1}}{\tan(\theta_{1})}=h_{1}\cot(\theta_{2})\\ & \to h_{2}\cot(\theta_{1})=h_{1}\cot(\theta_{2})+h_{1}\cot(\theta_{1})\\ & \to\dfrac{h_{2}\cot(\theta_{1})}{\cot(\theta_{2})+\cot(\theta_{1})}=h_{1} \end{align*}\]

Since \(h_{2}=100\), \(\theta_{1}=60^{\circ}\), and \(\theta_{2}=30^{\circ}\), we first want to evaluate \(\cot(60^{\circ})\) and \(\cot(30^{\circ})\). Recall

\[ \cot(\theta)=\dfrac{\cos(\theta)}{\sin(\theta)} \]

\[\begin{align*}\theta_{1} & =60^{\circ} & \theta_{2} & =30^{\circ}\\ \cos(60) & =\dfrac{1}{2} & \cos(30) & =\dfrac{\sqrt{3}}{2}\\ \sin(60) & =\dfrac{\sqrt{3}}{2} & \sin(30) & =\dfrac{1}{2}\\ \cot(60) & =\dfrac{1}{\sqrt{3}}\text{ or }\dfrac{\sqrt{3}}{3} & \cot(30) & =\sqrt{3} \end{align*}\]

\[\begin{align*}h_{1}=\dfrac{h_{2}\cot(\theta_{1})}{\cot(\theta_{2})+\cot(\theta_{1})} & \to h_{1}=\dfrac{100\cot(60^{\circ})}{\cot(30^{\circ})+\cot(60^{\circ})}\\ & \to h_{1}=\dfrac{100\cdot\dfrac{1}{\sqrt{3}}}{\sqrt{3}+\dfrac{1}{\sqrt{3}}}\\ & \to h_{1}=\dfrac{\dfrac{100}{\sqrt{3}}}{\frac{3+1}{\sqrt{3}}}\\ & \to h_{1}=\dfrac{100}{4}=25 \end{align*}\]

Therefore the height of Building B is 25 meters.

Example 14

Radar station A and B are on an east-west line, 8.6 km apart. Station A detects a plan at \(C\), on bearing of \(60^{\circ}\). Station B simultaneously detect the same plane, on a bearing of \(330^{\circ}\). Find the distance from B to C.

Solution:

First, we will draw a picture.

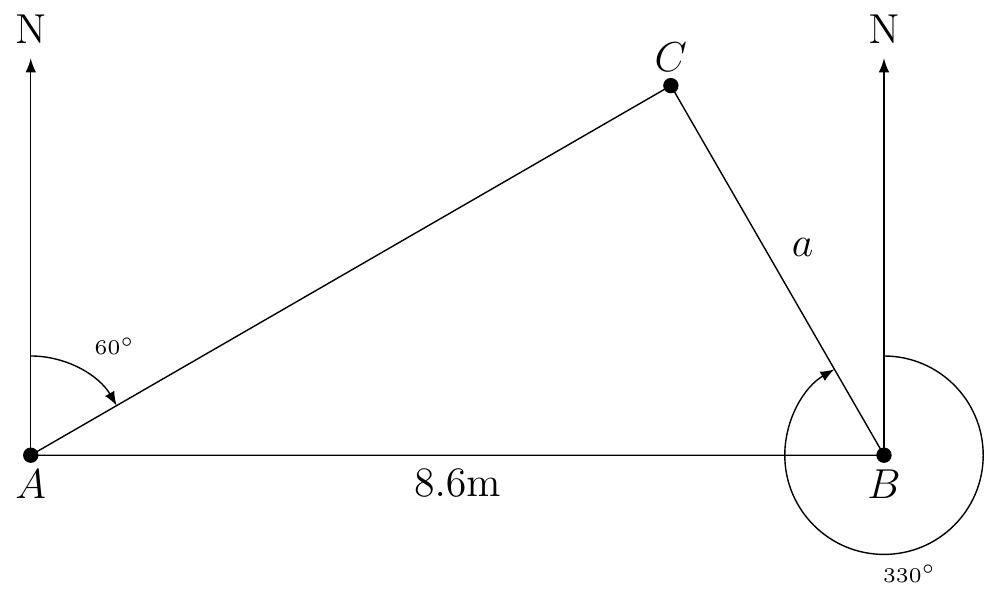
From the given information we know that \(\angle CAB=30^{\circ}\) and \(\angle CBA=330-270=60^{\circ}\). Therefore, \(\triangle ABC\) is a 30-60-90 right triangle.

We can then step up the following equation and solve for \(a\)

\[\begin{align*} \sin(30^{\circ}) & =\frac{a}{8.6}\\ a & =8.6\sin(30^{\circ})\\ & =8.6\cdot\frac{1}{2}\\ & =4.3 \end{align*}\]

Example 15

A ship leaves port and sails on a bearing of S\(45^{\circ}\)E for 2.5 hours. It then turns and sails on a bearing of N\(45^{\circ}\)E for 3 hours. If the ship’s rate is 18 knots (nautical miles per hour), find the distance that the ship is from port.

Solution:

First, we will draw a picture of the information.

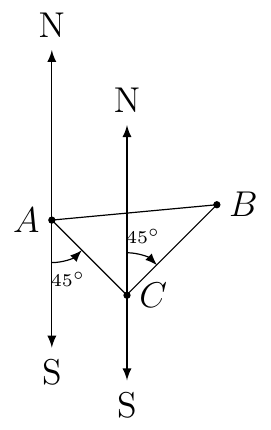
Second, we must show that \(\triangle ABC\) is a right triangle. By alternating interior angles we know the following:

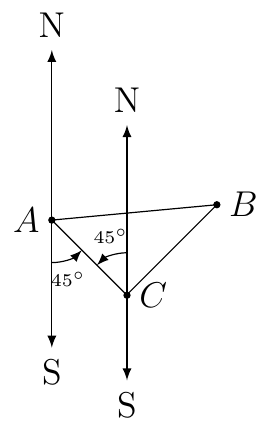
With the previous image we then now that \(\triangle ABC\) is a right triangle since \(45^{\circ}+45^{\circ}=90^{\circ}\).

Next, we will use the information to find the length of \(AC\) and \(BC\). We want to find \(AB\). By Pythagorean’s Theorem we know

\[ (AC)^{2}+(BC)^{2}=(AB)^{2} \]

We are given that the first part of the travel is 2.5 hours at 18 knots. Therefore,

\[ AC=2.5(18)=45.0 \]

Similarly, we know the second part is 3 hours at 18 knots. Therefore,

\[ BC=3(18)=54 \]

Therefore,

\[\begin{align*} AB & =\sqrt{45^{2}+54^{2}}\\ & =9\,\sqrt{61}\approx70.29 \end{align*}\]

Example 16

Bob needs to find the height of a building. From a given point on the ground, he finds that the angle of elevation to the top of the building is \(75^{\circ}\). He then walks back 35 feet. From the second point, the angle of elevation of the top of the building is \(50^{\circ}\). Find the height of the building in exact form.

Solution:

First, we will draw a picture:

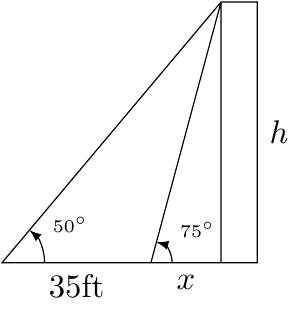
We want to solve for \(h\). We know

\[\begin{align*} \tan(50^{\circ}) & =\dfrac{h}{35+x}\\ \tan(75^{\circ}) & =\dfrac{h}{x} \end{align*}\]

Solving for \(h\) for both equations we have

\[\begin{align*} h & =35\tan(50^{\circ})+x\tan(50^{\circ})\\ h & =x\tan(75^{\circ}) \end{align*}\]

Next, setting the right hand side of the two equations equal to each other we have:

\[ 35\tan(50^{\circ})+x\tan(50^{\circ})=x\tan(75^{\circ}) \]

Solve for \(x\) we have

\[\begin{align*} 35\tan(50^{\circ})+x\tan(50^{\circ}) & =x\tan(75^{\circ})\\ 35\tan(50^{\circ}) & =x\tan(75^{\circ})-x\tan(50^{\circ})\\ & =x\left(\tan(75^{\circ}-\tan(50^{\circ})\right)\\ \dfrac{35\tan(50^{\circ})}{\tan(75^{\circ})-\tan(50^{\circ})} & =x \end{align*}\]

Since \(h=x\tan(75^{\circ})\) we have

\[\begin{align*} h & =\dfrac{35\tan(50^{\circ})}{\tan(75^{\circ})-\tan(50^{\circ})}\cdot\tan(75^{\circ})\\ & =\dfrac{35\tan(50^{\circ})\tan(75^{\circ})}{\tan(75^{\circ})-\tan(50^{\circ})}\\ & \approx61.2798 \end{align*}\]

Therefore, the exact height of the building is

\[ \dfrac{35\tan(50^{\circ})\tan(75^{\circ})}{\tan(75^{\circ})-\tan(50^{\circ})} \]

and the approximate height is 61.2798 feet.