Section 1.4

Definition 3 (Identities)

Identities are equations that are true for all values of the variables for which all expression are defined.

Definition 4 (Reciprocal Identities)

For all angles \(\theta\) for which both functions are defined, the following hold true:

\[\begin{align*} \sin (\theta) & = \frac{1}{\csc(\theta)} & \cos(\theta) & = \frac{1}{\sec(\theta)} & \tan(\theta) & = \frac{1}{\cot(\theta)}\\ \csc(\theta) & = \frac{1}{\sin(\theta)} & \sec(\theta) & = \frac{1}{\cos(\theta)} & \cot(\theta) & = \frac{1}{\tan(\theta)} \end{align*}\]

Remember in general \(f(5x)\ne 5f(x)\). This is also true for trig functions.

\[\cos(2x) \ne 2\cos(x)\]

Similarly,

\[\cos(x+y) \ne \cos(x)+\sin(y)\]

The signs for the sine and cosine function are as follows.

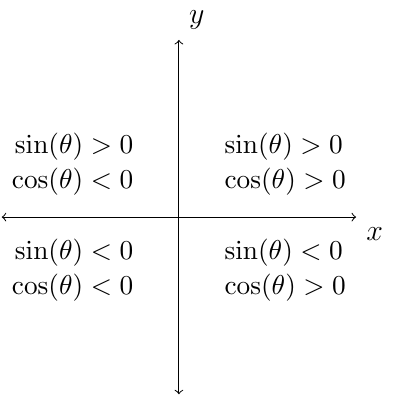
Let \(k\) be any integer.

Trig Function	Domain	Range
\(\sin(\theta)\),\(\cos(\theta)\)	\(\mathbb{R}\)	\([-1,1]\)
\(\tan(\theta)\)	\(x\ne \frac{\pi}{2}+\pi k\)	\(\mathbb{R}\)
\(\cot(\theta)\)	\(x\ne \pi + \pi k\)	\(\mathbb{R}\)
\(\sec(\theta)\)	\(x\ne \frac{\pi}{2} + \pi k\)	\((-\infty,-1]\cup[1,\infty)\)
$\csc(\theta)	\(x\ne \pi + \pi k\)	\((-\infty,-1]\cup[1,\infty)\)

Theorem 2 (Quotient Identities)

For all angles \(\theta\) for which the denominators are not zero, the follow are true.

\[\begin{align*} \frac{\sin(\theta)}{\cos(\theta)} & = \tan(\theta) & \frac{\cos(\theta)}{\sin(\theta)} & = \cot(\theta) \end{align*}\]

Theorem 3 (Pythagorean Identities)

For all angles \(\theta\) for which the function values are defined, the following are true.

\[\sin^2(\theta)+\cos^2(\theta) = 1\]

\[\tan^2(\theta)+1=\sec^2(\theta)\]

\[\cot^2(\theta)+1=\csc^2(\theta)\]