Section 3.4

The following image will drive the conversation for this section:

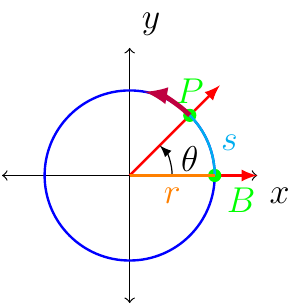
The path of the point P what moves at a constant speed along the circle.

Definition 11 (Linear Speed)

The measure of how fast the position of \(P\) is changing is linear speed. If \(v\) represents linear speed, then

\[ \text{speed}=v=\dfrac{\text{distance}}{\text{time}}=\dfrac{s}{t} \]

where \(s=r\theta\).

Definition 12 (Angular Speed)

As point \(P\) moves along the circle, the ray \(\overrightarrow{OP}\) is the terminal side of \(\angle POB\), the measure of the angle changes as \(P\) moves along the circle.

The measure of how fast \(\angle POB\) is changing is called the angular speed and is defined as

\[ \omega=\dfrac{\theta}{t} \]

where \(\theta\) must be in units of radians.

Linear speed is defined as

\[ v=\frac{s}{t} \]

where \(s=r\theta\). This yields:

\[\begin{align*} v & =\dfrac{s}{t}\\ & =\dfrac{r\theta}{t}\\ & =r\cdot\frac{\theta}{t}\\ & =r\omega \end{align*}\]

Therefore, \(v=\frac{s}{t}\) or \(v=r\omega\).

Example 22

Suppose that \(P\) is on a circle with radius 15 inches and \(\overrightarrow{OP}\) is is rotating with angular speed of \(\frac{\pi}{12}\) radians per second.

Find the angle generated by \(P\) in 10 seconds.

Solution:

Since \(\omega=\frac{\pi}{12}\) and \(\omega=\frac{\theta}{t}\) where \(t=10\) we have

\[\begin{align*} \frac{\pi}{12} & =\frac{\theta}{10}\\ \theta & =\frac{10\pi}{12}\\ & =\frac{5\pi}{6} \end{align*}\]

Find the distance traveled by \(P\) along the circle in 10 seconds.

Solution:

Given \(r=15\) and \(\theta=\frac{5\pi}{6}\) we have

\[\begin{align*} s & =r\theta\\ & =15\cdot\frac{5\pi}{6}\\ & =\frac{25\pi}{2} \end{align*}\]

The units would be inches.

Find the linear speed of \(P\) in inches per second.

Solution:

First, we could use \(v=r\omega\) where \(r=15\) and \(\omega=\frac{\pi}{12}\).

This gives

\[\begin{align*} v & =15\cdot\frac{\pi}{12}\\ & =\frac{5\pi}{4} \end{align*}\]

and the units would be inches per second.

Alternatively, we could use the \(v=\frac{s}{t}\) where

\[ s=15\cdot\frac{5\pi}{6}=\frac{25\pi}{2} \]

and \(t=10.\) Thus,

\[\begin{align*} v & =\frac{\frac{25\pi}{2}}{10}\\ & =\frac{25\pi}{20}\\ & =\frac{5\pi}{4} \end{align*}\]

The units is still inches per second.

Example 23

A belt runs a pulley of radius 5 centimeters at 120 revolutions per minute.

Find the angular speed of the pulley in radians per second.

Solution:

Since 1 revolution is \(2\pi\) and 1 minute is 60 seconds, we have the following using dimensional analysis

\[\begin{align*} \frac{120\text{ rev}}{1\text{ min}}\cdot\left(\frac{1\text{ min}}{1\text{ min}}\right)\cdot\left(\frac{1\text{ rev}}{1\text{ rev}}\right) & =\frac{120\cancel{\text{ rev}}}{1\cancel{\text{ min}}}\cdot\left(\frac{1\cancel{\text{ min}}}{60\text{ sec}}\right)\cdot\left(\frac{2\pi\text{ rad}}{1\cancel{\text{ rev}}}\right)\\ & =\frac{120\cdot(2\pi)}{60}\frac{\text{rad}}{\text{sec}}\\ & =4\pi\frac{\text{rad}}{\text{sec}} \end{align*}\]

Find the linear speed of the belt in centimeters per second.

Solution:

Since \(\omega=4\pi\) and \(r=5\) we have

\[\begin{align*} v & =r\omega\\ & =5\cdot(4\pi)\\ & =20\pi \end{align*}\]

centimeters per seconds.