Section 1.3

Theorem 1

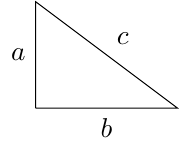
If a triangle is a right triangle, then \(a^2+b^2=c^2\).

If the sides of a triangle satisfy \(a^2+b^2=c^2\), then the triangle is a right triangle.

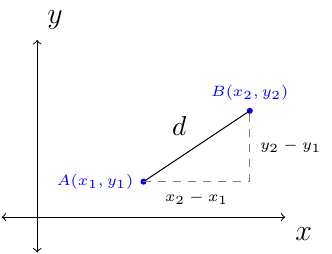
By Pythagorean Thoerem we have the following distance forumla:

\[d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]

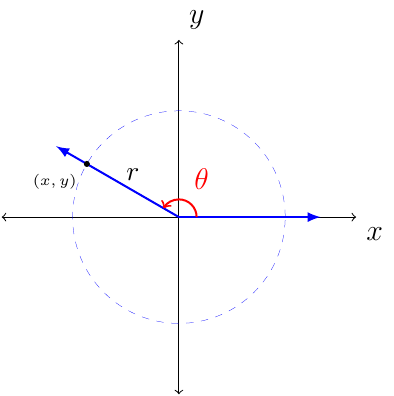
From the image notice that \(r=\sqrt{x^2+y^2}\).

The following definition is associated with the above image showing a point in space with a radius and angle, \(\theta\).

Definition 2

Let \((x,y)\) be a point other than the origin on the terminal side of angle \(\theta\) in standard position.

The distance from the point to the origin is \(r=\sqrt{x^2+y^2}\). The six trigonometric functions of \(\theta\) are as follows.

\[\begin{align*} \cos(\theta) & =\frac{x}{r} & \sin(\theta)=\frac{y}{r} & \tan(\theta)=\frac{y}{x}\text{ ($x\ne0$)}\\ \sec(\theta) & =\frac{r}{x} & \csc(\theta)=\frac{r}{y} & \cot(\theta)=\frac{x}{y}\text{ ($y\ne0$)} \end{align*}\]

Example 1

The terminal side of an angle \(\theta\) in standard position passes through the point \((4,3)\). Find the values of the six trigonometric functions.

Solution:

In order to find the values of the six trig functions we need to know what \(x\), \(y\), and \(r\) equals. We are given \(x=4\) and \(y=3\). To find \(r\) we find the distance between the point \((4,3)\) and the origin, \((0,0)\).

\[\begin{align*} r & = \sqrt{4^2 + 3^2}\\ & = \sqrt{16+9}\\ & = \sqrt{25}\\ & = 5 \end{align*}\]

Therefore, we have \(x=4\), \(y=3\), and \(r=5\). Using the previous definition we have:

\[\begin{align*} \cos(\theta) & = \frac45 & \sin(\theta) & = \frac35 & \tan(\theta) & = \frac34\\ \sec(\theta) & = \frac54 & \csc(\theta) & = \frac53 & \cot(\theta) & = \frac43 \end{align*}\]

The terminal side of an angle \(0^{\circ}\) in standard position would pass through any point along the positive \(x\)-axis. The radius for this situation would then be \(r=x\). Therefore, we have the following conclusion for evaluating the six trig functions when \(\theta=0^{\circ}\).

\[\begin{align*} \cos(0^{\circ}) & = \frac{x}{x}=1 & \sin(0^{\circ}) & = \frac{0}{x}=0 & \tan(0^{\circ}) & = \frac{0}{x}=0\\ \sec(0^{\circ}) & = 1 & \csc(0^{\circ}) & = \text{UND} & \cot(0^{\circ}) & = \text{UND} \end{align*}\]

\(\theta\)	\(\cos(\theta)\)	\(\sin (\theta)\)	\(\tan(\theta)\)	\(\sec(\theta)\)	\(\csc(\theta)\)	\(\cot(\theta)\)
\(0^{\circ}\)	1	0	0	1	UND	UND
\(90^{\circ}\)	0	1	UND	UND	1	0
\(180^{\circ}\)	-1	0	0	-1	UND	UND
\(270^{\circ}\)	0	-1	UND	UND	-1	0
\(360^{\circ}\)	1	0	0	1	UND	UND