Section 5.1

In this section we recall the fundamental identities for trigonometric functions.

For, example \(\cos(-x)=\cos(x)\) and \(\sin(-x)=-\sin(x)\). Later, will we also need to remember:

Given \(x^2+y^2=r^2\) (a circle with radius \(r\)), we have,

\[\begin{align*} \cos(\theta)=\frac{x}{r} && \sin(\theta)=\frac{y}{r} && \tan(\theta)=\frac{y}{x}\\ \sec(\theta)=\frac{r}{x} && \csc(\theta)=\frac{r}{y} && \cot(\theta)=\frac{x}{y} \end{align*}\]

We also have the reciprocal identities

\[\begin{align*} \cot(\theta)=\frac{1}{\tan(\theta)} && \sec(\theta)=\frac{1}{\cos(\theta)} && \csc(\theta)=\frac{1}{\sin(\theta)} \end{align*}\]

The quotient identities

\[\begin{align*} \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)} && \cot(\theta)=\frac{\cos(\theta)}{\sin(\theta)} \end{align*}\]

One of the most important identities that will be used through this chapter is

\[\cos^2(\theta)+\sin^2(\theta)=1\]

By dividing both sides by \(\cos^2(\theta)\) we then get

\[1+\tan^2(\theta)=\sec^2(\theta)\]

Or dividing both sides by \(\sin^2(\theta)\) we then get

\[\cot^2(\theta)+1=\csc^2(\theta)\]

As a consequence of those three identities we have

\[\begin{align*} \cos^2(\theta)&=1-\sin^2(\theta) & \sin^2(\theta)&=1-\cos^2(\theta)\\ &=(1-\sin(\theta))(1+\sin(\theta)) && =(1-\cos(\theta))(1+\cos(\theta))\\\\ \tan^2(\theta) & =\sec^2(\theta)-1 & \cot^2(\theta) & = \csc^2(\theta)-1 \end{align*}\]

This may look like a lot to remember; however, only one identity must be memorized: \(\cos^2(\theta)+\sin^2(\theta)=1\). All of the other identities “spawn” from that identity. We call this identity, Pythagorean Identity.

Example 28

If \(\tan(\theta)=\frac{1}{3}\) and \(\theta\) is in quadrant three, then find \(\sin(\theta)\) and \(\cos(\theta)\).

Solution:

First, we will construct the triangle involving this situation:

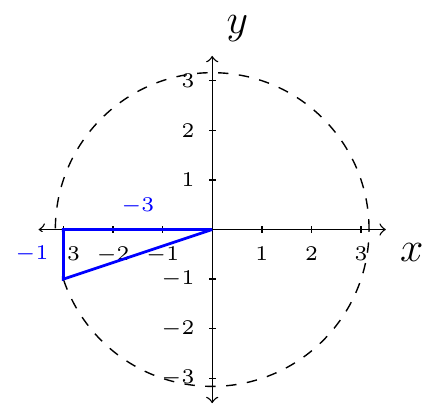
The hypotenuse of this triangle is

\[\begin{align*} h^2 & = (-3)^2+(-1)^2\\ & = 10\\ h & = \sqrt{10} \end{align*}\]

We have \(x=-3\), \(y=-1\), and \(h=\sqrt{10}\). Therefore,

\[\cos(\theta)=\frac{-3}{\sqrt{10}}\]

and

\[\sin(\theta)=\frac{-1}{\sqrt{10}}\]

Example 29

Write \(\dfrac{1+\tan^{2}(\theta)}{1-\sec^{2}(\theta)}\) in terms of \(\sin(\theta)\) and \(\cos(\theta)\). Then simplify the expression so that there are no quotients by using the quotient identities or reciprocal identities.

Solution:

First, we will directly substitute cosine and sine into the original expression

\[ \dfrac{1+\tan^{2}(\theta)}{1-\sec^{2}(\theta)}=\dfrac{1+\dfrac{\sin^{2}(\theta)}{\cos^{2}(\theta)}}{1-\dfrac{1}{\cos^{2}(\theta)}}. \]

Second, we will simplify

\[\begin{align*} \dfrac{1+\dfrac{\sin^{2}(\theta)}{\cos^{2}(\theta)}}{1-\dfrac{1}{\cos^{2}(\theta)}} & =\dfrac{\frac{\cos^{2}(\theta)+\sin^{2}(\theta)}{\cos^{2}(\theta)}}{\frac{\cos^{2}(\theta)-1}{\cos^{2}(\theta)}}\\ & =\dfrac{\cos^{2}(\theta)+\sin^{2}(\theta)}{\cos^{2}(\theta)-1}\\ & =\dfrac{1}{-\left(1-\cos^{2}(\theta)\right)}\\ & =\dfrac{1}{-\sin^{2}(\theta)}. \end{align*}\]

Finally, we will rewrite \(-\dfrac{1}{\sin^{2}(\theta)}\).

\[ -\dfrac{1}{\sin^{2}(\theta)}=-\csc^{2}(\theta). \]