Section 3.3

Definition 10

A circle centered at \((0,0)\) and has a radius of \(1\) unit is called the unit circle.

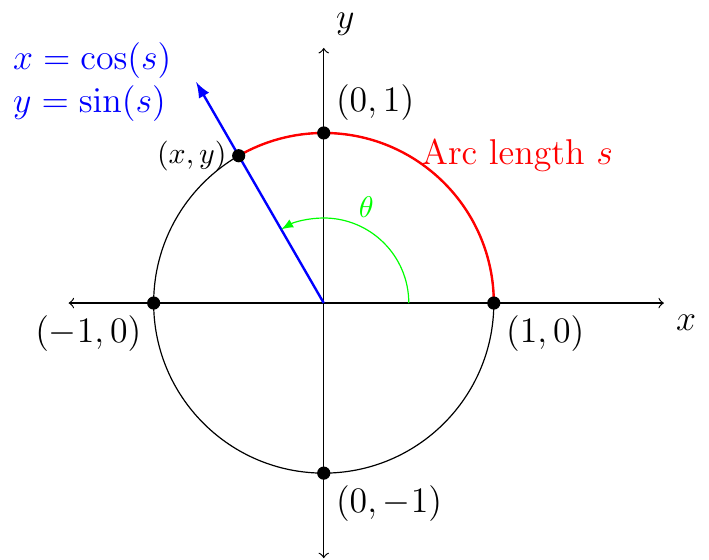
The following functions are defined for any real number \(s\) represented by a directed arc on the unit circle.

\[\begin{align*}\cos(s) & =x & \sin(s) & =y & \tan(s) & =\dfrac{y}{x}\\ \sec(s) & =\frac{1}{x} & \csc(s) & =\frac{1}{y} & \cot(s) & =\dfrac{x}{y} \end{align*}\]

The sine and cosine function is the set of all \(x\) such that \(x\) is an element of the real numbers.

Tangent and secant function is the set of all \(x\) such that \(x\ne(2n+1)\cdot\frac{\pi}{2}\) where \(n\) is any integer,

\[ \{x\,|\,n\in\Z\land x\ne(2n+1)\cdot\frac{\pi}{2}\}. \]

Cotangent and cosecant function is the set of all \(x\) such that \(x\ne(2n)\cdot\frac{\pi}{2}\) where \(n\) is any integer,

\[ \{x\,|\,n\in\Z\land x\ne(2n)\cdot\frac{\pi}{2}\}=\{x\,|\,n\in\Z\land x\ne n\pi\} \]

Example 21

First, find the coterminal angle such that \(\theta_{c}\in[0,2\pi)\), then find the reference angle \(\theta'\).

\(\frac{13\pi}{4}\)

Solution:

\[\begin{align*} \frac{13\pi}{4}-2\pi & =\frac{5\pi}{4}\in[0,2\pi)\implies\theta_{c}=\frac{5\pi}{4}\\ \theta_{c}=\frac{5\pi}{4} & \implies\theta'=\frac{\pi}{4} \end{align*}\]

\(\frac{17\,\pi}{6}\)

Solution:

\[\begin{align*} \dfrac{17\pi}{6}-2\pi & =\frac{5\pi}{6}\in[0,2\pi)\implies\theta_{c}=\dfrac{5\pi}{6}\\ \theta_{c}=\frac{5\pi}{6} & \implies\theta'=\frac{\pi}{6} \end{align*}\]

\(\frac{13\,\pi}{3}\)

Solution:

\[\begin{align*} \dfrac{13\pi}{3}-2\pi & =\frac{7\pi}{3}\notin[0,2\pi)\\ \dfrac{7\pi}{3}-2\pi & =\frac{\pi}{3}\in[0,2\pi)\implies\theta_{c}=\frac{\pi}{3}\\ \theta_{c}=\frac{\pi}{3} & \implies\theta'=\frac{\pi}{3} \end{align*}\]

\(-\frac{2\,\pi}{3}\)

Solution:

\[\begin{align*} -\frac{2\pi}{3}+2\pi & =\frac{4\pi}{3}\in[0,2\pi)\implies\theta_{c}=\dfrac{4\pi}{3}\\ \theta_{c}=\dfrac{4\pi}{3} & \implies\theta'=\frac{\pi}{3} \end{align*}\]

\(-\frac{19\,\pi}{6}\)

Solution:

\[\begin{align*} -\dfrac{19\pi}{6}+2\pi & =-\frac{7\pi}{6}\notin[0,2\pi)\\ -\dfrac{7\pi}{6}+2\pi & =\frac{5\pi}{6}\in[0,2\pi)\implies\theta_{c}=\dfrac{5\pi}{6}\\ \theta_{c}=\dfrac{5\pi}{6} & \implies\theta'=\dfrac{\pi}{6} \end{align*}\]

\(-\frac{\pi}{4}\)

Solution:

\[\begin{align*} -\frac{\pi}{4}+2\pi & =\frac{7\pi}{4}\in[0,2\pi)\implies\theta_{c}=\dfrac{7\pi}{4}\\ \theta_{c}=\dfrac{7\pi}{4} & \implies\theta'=\dfrac{\pi}{4} \end{align*}\]

{prf:example}

label:

evalTrigRadExam

Find the exact values of the following:

\(\cos(\frac{11\,\pi}{3})\)

Solution:

\[\begin{align*} \dfrac{11\pi}{3}-2\pi & =\frac{5\pi}{3}\in[0,2\pi)\\ & \implies\theta_{c}=\dfrac{5\pi}{3}\land\theta_{c}\in(\frac{3\pi}{2},2\pi)\subseteq[0,2\pi)\\ & \implies\cos(\theta_{c})>0\\ \\\theta_{c}=\frac{5\pi}{3} & \implies\theta'=\frac{\pi}{3}\\ \\\therefore\cos(\frac{11\pi}{3}) & =\cos(\frac{\pi}{3})\\ & =\dfrac{1}{2} \end{align*}\]

\(\sin(-\frac{5\,\pi}{4})\)

Solution:

\[\begin{align*} -\dfrac{5\pi}{4}+2\pi & =\frac{3\pi}{4}\in[0,2\pi)\\ & \implies\theta_{c}=\dfrac{3\pi}{4}\land\theta_{c}\in(\frac{\pi}{2},\pi)\subseteq[0,2\pi)\\ & \implies\sin(\theta_{c})>0\\ \\\theta_{c}=\dfrac{3\pi}{4} & \implies\theta'=\dfrac{\pi}{4}\\ \\\therefore\sin(-\frac{5\pi}{4}) & =\sin(\frac{\pi}{4})\\ & =\dfrac{\sqrt{2}}{2} \end{align*}\]

\(\tan(\frac{11\,\pi}{2})\)

Solution:

\[\begin{align*} \dfrac{11\pi}{2}-2\pi & =\frac{7\pi}{2}\notin[0,2\pi)\\ \dfrac{7\pi}{2}-2\pi & =\frac{3\pi}{2}\in[0,2\pi)\\ & \implies\theta_{c}=\dfrac{3\pi}{2} \end{align*}\]

If we consider \(\tan(\frac{3\pi}{2})\) we would need to consider the fact that \(\tan(\frac{3\pi}{2})=\dfrac{\sin(\frac{3\pi}{2})}{\cos(\frac{3\pi}{2})}\) and we must notice that \(\cos(\frac{3\pi}{2})=0\). Therefore, \(\tan(\dfrac{3\pi}{2})\) is undefined, which also means \(\tan(\frac{11\pi}{2})\) is undefined.